Hierbij een beetje wiskunde achtergrond bij de berekening van Novi. Beschouw de evenementen (stochastische variabelen) A = vorst zondag, B = vorst maandag en C = vorst dinsdag. We willen nu de kans berekenen dat het vriest op een van die dagen. In wiskundige notatie zou dit de kans P(A ∪ B ∪ C), ofwel de kans op de unie van alle dagen. Je kan dit in een Venn diagram voorstellen, waarbij we eigenlijk de totale oppervlakte willen bepalen van A, B en C.
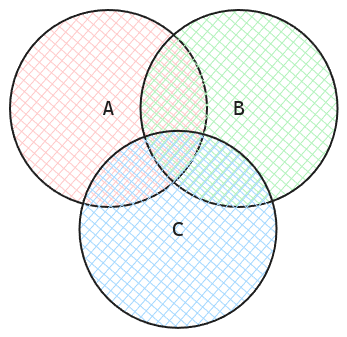
Als we veronderstellen dat A, B en C onafhankelijk zijn, kunnen we gebruik maken van het feit dat P(A ∩ B) = P(A) * P(B) per definitie van onafhankelijke stochastische variabelen. De kans dat het vriest op zondag én maandag P(A ∩ B) is dus het product van de kans dat het vriest op zondag P(A) en de kans dat het vriest op maandag P(B).
De totale kans kunnen we dan bepalen door alle kansen P(A), P(B) en P(C) op te tellen. Maar dan hebben we de overlappende gebieden dubbel geteld, dus moeten we P(A ∩ B), P(A ∩ C) en P(B ∩ C) aftrekken. Maar dan hebben we het middenste deel waar A, B en C overlappen, eenmaal te veel afgetrokken, dus moeten we dat nogmaals optellen.
Dus P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C), wat we dan kunnen herschrijven gebruik makende van dat A, B en C onafhankelijk zijn. Dus P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A) * P(B) - P(A) * P(C) - P(B) * P(C) + P(A) * P(B) * P(C).
Voor P(A)=2%, P(B)=10% en P(C)=10% geeft dat dan 20.6%.
Een belangrijk detail is dat we ervan uit gaan dat A, B en C onafhankelijk zijn. Maar je kan beargumenteren dat dat hier niet het geval is, waardoor de berekening eigenlijk niet op gaat. Een alternatieve definitie: A en B zijn onafhankelijk als en slechts als P(B | A) = P(B). In ons geval betekent dit dat de kans op vorst op maandag gegeven dat het al gevroren heeft op zondag P(B | A) gelijk moet zijn aan de kans op vorst op maandag P(B).
Een tegenargument zou kunnen zijn dat als het reeds gevroren heeft op zondag, dat de kans dat het op maandag nog eens vriest groter kan zijn omdat de atmosferische condities duidelijk goed zijn. Een ander argument zou als volgt kunnen gaan: de leden in het ensemble die vorst laten zien op zondag laten relatief vaker ook vorst zien op maandag en/of dinsdag dan de rest van de leden. In dat geval zijn A, B en C niet onafhankelijk en zal de kansberekening fout zijn.